Интересные факты
 Это растение не случайно напоминает пучок проводов, торчащий из земли. Fenestraria, растущая в засушливых районах Африки, почти целиком прячется в песке, под поверхностью земли. Но как и любому растению, ей положено фотосинтезировать. Как же это делать, когда ты с головой засыпан песком? Фенестрария производит самое настоящее оптоволокно из кристаллов щавелевой кислоты, выставляет кончики светопроводящих отростков наружу и таким образом обеспечивает поставку солнечных лучей в свои подземные фотосинтезирующие фабрики! Это растение не случайно напоминает пучок проводов, торчащий из земли. Fenestraria, растущая в засушливых районах Африки, почти целиком прячется в песке, под поверхностью земли. Но как и любому растению, ей положено фотосинтезировать. Как же это делать, когда ты с головой засыпан песком? Фенестрария производит самое настоящее оптоволокно из кристаллов щавелевой кислоты, выставляет кончики светопроводящих отростков наружу и таким образом обеспечивает поставку солнечных лучей в свои подземные фотосинтезирующие фабрики! |
 В квантовой теории поля есть важный для понимания CP-нарушений класс фейнмановских диаграмм, описывающих однопетлевой процесс, в котором кварк временно меняет аромат. В квантовой теории поля есть важный для понимания CP-нарушений класс фейнмановских диаграмм, описывающих однопетлевой процесс, в котором кварк временно меняет аромат.И при чём, казалось бы, тут пингвины?.. |
 Словосочетание «Finger of death» как нельзя лучше подходит этой зловещей ледяной «сосульке», несущей смерть всему на своём пути... Словосочетание «Finger of death» как нельзя лучше подходит этой зловещей ледяной «сосульке», несущей смерть всему на своём пути...См. видео: → Брайникл |
|
Человек склонен объяснять свои успехи своими внутренними достоинствами, а неудачи — внешними обстоятельствами. А чужие успехи и неудачи — ровно наоборот! — Он опоздал на встречу? Ай-ай-ай, какой он непунктуальный и безответственный. |
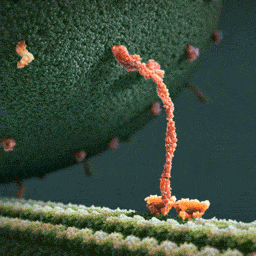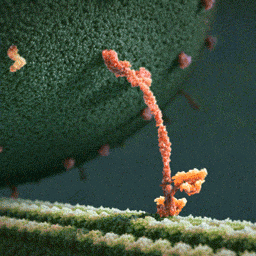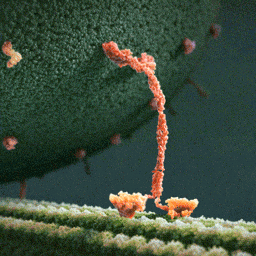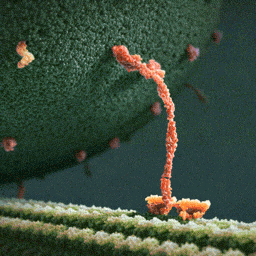 В клетках организмов маленькие молекулы типа газов или глюкозы приносятся к месту назначения просто броуновским движением. Но для доставки крупных сооружений внутри клеток строятся специальные транспортные магистрали — микротрубочки, по которым вышагивают челноки-перевозчики — моторные белки (кинезины), тянущие за собой вагоны с грузом — везикулы. В клетках организмов маленькие молекулы типа газов или глюкозы приносятся к месту назначения просто броуновским движением. Но для доставки крупных сооружений внутри клеток строятся специальные транспортные магистрали — микротрубочки, по которым вышагивают челноки-перевозчики — моторные белки (кинезины), тянущие за собой вагоны с грузом — везикулы.Двигаются они, расходуя энергию универсального биологического топлива — АТФ. По одной молекуле АТФ на каждый шаг. На картинке — шагающая молекула белка перетаскивает по микротрубочке мембранный пузырёк с большим полезным грузом от одной части внутри клетки к другой. Дальше ещё видео (в том числе более точное): |
 Капля стекла, самого обычного стекла, не сапфирового и не прослоенного пуленепробиваемыми поликарбонатами, способно выдерживать удары молота и даже давление мощного пресса. Но, подобно другим ахиллесам, имеет свою пяту — стоит отломить у капли тонкий хвостик, как она целиком взрывается, разлетаясь на мельчайшие осколки. Подробнее дальше: Капля стекла, самого обычного стекла, не сапфирового и не прослоенного пуленепробиваемыми поликарбонатами, способно выдерживать удары молота и даже давление мощного пресса. Но, подобно другим ахиллесам, имеет свою пяту — стоит отломить у капли тонкий хвостик, как она целиком взрывается, разлетаясь на мельчайшие осколки. Подробнее дальше: |
 В конце 1960-х годов ректор одного из советских вузов, посоветовавшись в ЦК КПСС, издал приказ, рекомендующий преподавателям института отпускать бороды и длинные волосы, носить рваные джинсы и сандалии на босу ногу. В конце 1960-х годов ректор одного из советских вузов, посоветовавшись в ЦК КПСС, издал приказ, рекомендующий преподавателям института отпускать бороды и длинные волосы, носить рваные джинсы и сандалии на босу ногу. |
 В джунглях Амазонии живёт племя охотников-собирателей Пирахан. Оно вполне цивилизованно, торгует с соседними племенами и пользуется благами цивилизации (вплоть до телевизора). Но в их языке (и вообще в понятийном аппарате) нет числительных — ни количественных, ни порядковых. Вместо «один», «два», «три» и т.д. они использут всего два слова, приблизительно означающие «мало-поменьше» и «много-побольше». В джунглях Амазонии живёт племя охотников-собирателей Пирахан. Оно вполне цивилизованно, торгует с соседними племенами и пользуется благами цивилизации (вплоть до телевизора). Но в их языке (и вообще в понятийном аппарате) нет числительных — ни количественных, ни порядковых. Вместо «один», «два», «три» и т.д. они использут всего два слова, приблизительно означающие «мало-поменьше» и «много-побольше».<На фото — охотник племени пытается посчитать, сколько рыболовных крючков ему показывают.> |
 На открытых горных просторах и в наполненных разнородным шумом джунглях условия акустики привели к возникновению у людей языков, использующих для передачи информации разнотоновый свист, очень напоминающий пение птиц. На открытых горных просторах и в наполненных разнородным шумом джунглях условия акустики привели к возникновению у людей языков, использующих для передачи информации разнотоновый свист, очень напоминающий пение птиц. |
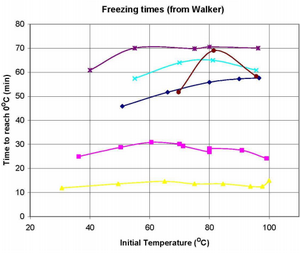 В 1963 году один африканский мальчик на школьном уроке по кулинарии делал мороженое и заметил странную вещь — горячая смесь в холодильнике почему-то замерзала быстрее холодной. Через несколько лет его школу посетил профессор Осборн, приглашённый из университета, чтобы прочитать лекцию по физике. По её окончании тот ученик задал лектору вопрос: «Если взять две одинаковых ёмкости, заполненных водой, одну с температурой 35 °C, а вторую около 100 °C, то почему та, что изначально была горячее, замёрзнет первой?» — одноклассники и школьный учитель рассмеялись над такой глупостью. В 1963 году один африканский мальчик на школьном уроке по кулинарии делал мороженое и заметил странную вещь — горячая смесь в холодильнике почему-то замерзала быстрее холодной. Через несколько лет его школу посетил профессор Осборн, приглашённый из университета, чтобы прочитать лекцию по физике. По её окончании тот ученик задал лектору вопрос: «Если взять две одинаковых ёмкости, заполненных водой, одну с температурой 35 °C, а вторую около 100 °C, то почему та, что изначально была горячее, замёрзнет первой?» — одноклассники и школьный учитель рассмеялись над такой глупостью.Но профессор, очнувшись от первоначального удивления, вернулся в лабораторию и решил таки провести этот опыт … и увидел, что эффект действительно подтверждается! С тех пор этот удивительный парадокс, до сих пор до конца не объяснённый, носит имя того школьника — «эффект Мпембы». |