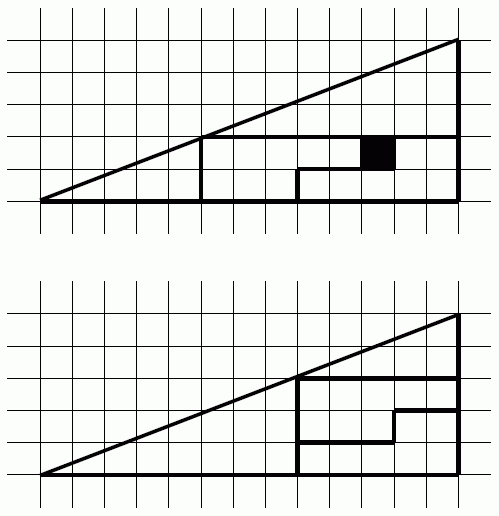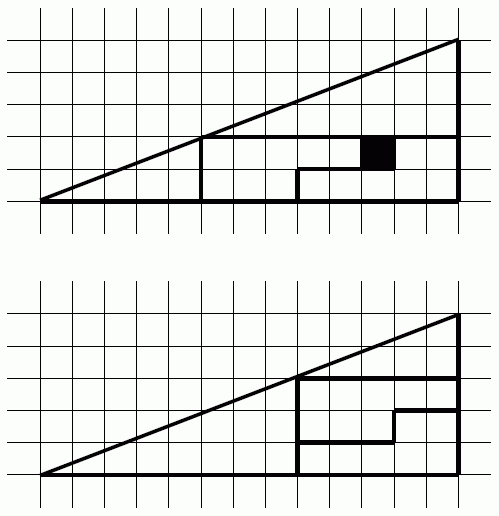35. Разрезание треугольника

Обман зрения
В данном случае, треугольники внутри большого треугольника лишь кажутся одинковыми, на самом деле несколько миллиметров разницы имеет место. На всей длине, эта разница дает необходимую площадь одного квадрата

Нет
Треугольники внутри большого треугольника — абсолютно одинаковы.

Толстые линии -- это же линии разреза. У них нулевая толщина.

ответ
Треугольники внутри большого треугольника не подобны. Значит их гипотенузы не параллельны. Значит у большого треугольника гипотенуза является не прямой, а ломаной. На нижнем рисунке она вогнута, а на верхнем выгнута.

Хм... Ну вообще странно, что S(площадь) большого треугольника = 0,5*13*5=32,5 , а сумма площадей состовляющих его фигур = 12+5+8+7=32 (сначала) и 12+5+8+7+1=33 (потом).
Хотя наверное все дело в том, что при перестановке 2 треугольников оставщееся пространство имеет площадь не 15, а 16 (вот в ней и получается 1 лишний квадратик)
Наверное эту загадку нам оставили марсиане)))

Ха! Допер!

странная штука получается!
уже всё перемножил перевычетал,собирался было интегрировать что-нибудь и тут нарвался:
Левые углы треугольников(тех треугольников что внутри больших) равны(по теореме о накрест-лежащих и соответсвенных углах,если углубляться).Назовём их Z1 и Z2 -левые углы малого и большого треугольников соответственно.Стало быть SinZ1=SinZ2.
рассмотрим верхнюю фигуру,внутри которой снизу малый треугольник,сверху -большой:
SinZ1=2:5 = SinZ2=3:8 0,4 не=0,375
Следовательно Z1>Z2,значит гипотенуза верхней фигуры вовсе не прямая линия и вовсе не гипотенуза а два отрезка как бы образуещие выпуклую линию.Если аналогично рассмотреть нижнюю фигуру,то гипотенуза окажется "вогнутой".А та самая пустота в виде одной клеточки это есть разница между Выпуклостью и вогнутостью,площадь которой равна единице.Просто лень писать дальнейший расчёт.

"Наверное эту загадку нам оставили марсиане)))"
Этот треугольник называется треугольником Керри
А вот еще геометрическая задача
Разделите квадрат на остроугольные треугольники!(штук на восемь)

хыы какие марсиане? :))))
Тут просто прикол! На верхней картинке изображен не треугольник а четырехугольник! на "гипотенузе" у него вмятина получается так как углы у больших треугольников разные. А на нижнем рисунке и вправду треугольник изображен. :))

Зрительная иллюзия
Рассмотрим верхний прямоугольный треугольник (А). Длина его катетов: а = 13, b = 5.
Разбиваем нижний катет (а) на два отрезка: 5 и 8, и из этой точки проводим перпендикуляр до гипотенузы. Получаем прямоугольный треугольник А1 с катетами: а1 = 5 и b1.
Из точки пересечения перпендикуляра с гипотенузой проводим линию, параллельную нижнему катету (а). Получаем прямоугольный треугольник А2 с катетами: а2 = 3 и b2.
Рисунок "толкает" наше зрение на признание, что катет b1 = 2, а катет b2 = 3. Проверим это.
Из подобия треугольников А, А1 и А2 следует, что: a/b = a1/b1 = a2/b2. Подставим вместо b1 и b2 значения, которые нам "подсказывает" наше зрение:
a/b = 13/5 = 2.6; a1/b1 = 5/2 = 2.5; a2/b2 = 8/3 = 2.6(6).
Из отношение a1/b1 = 2.5 следует, что катет b1>2 (a1/b1<a/b). Из отношение a2/b2 = 2.6(6) следует, что катет b2<3 (a2/b2>a/b). Второй вывод можно было сразу сделать из первого (b1+b2=5).
Из этого следуют неутешительные выводы (для патентования):
1) Прямоугольник (А3), ограниченный треугольниками А1 и А2 имеет стороны а3 = 8 и b3 > 2.
И значит, фигуры, вырезанные из него с удалением "черного квадрата" не смогут образовать новый прямоугольник со сторонам 5 и 3 (нижний рисунок).
2) Гипотенузы треугольников А1 и А2 не смогут образовать на нижнем рисунке прямую линию, так как в этом случае должно выполняться равенство:
a1/b1 = a2/b2, мы же имеем 2.5 < 2.6(6).
Подсчитаем, насколько наше зрение обманывает нас:
Площадь верхнего прямоугольного треугольника (А) равна 32.5 (13*5/2), нижней фигуры = 31.5. Разница между ними составляет около 3%.
Статистическая погрешность.

мой ответ
дело в том, что фигура, собранная из других фигур не являтся треугольником, а просто каким-то набором фигур))

Стыдно, eruditor, стыдно!
Дело в том, что гипотенуза большого треугольника не проходит ни через точку (5,2) ни через точку (8,3) что легко понять, потому что иначе она бы проходила и через точки (-1,0) и (14,5). В основе парадокса лежит близость чисел 2.6 и 3.))))

то есть ни один из предполагаемых прямоугольников со сторонами 3,5 и 2,8 не лежат углами на гипотенузах больших треугольников.

ВСё элементарно:
Данная большая фигура - это не треугольник, а четырёхугольник! Почему? Посмотрив на 2 маленьких треугольника. По идее они должны быть подобны, но они НЕ ПОДОБНЫ! У них отношениу катетов разное: 8\3<>5\2. Этим всё доказано!

Стыдно!!! мне За вас!!! Но не за Bugaboo!! :)
Молочек!! я только что прочитал, мне кажется очевидным что надо было сразу проверить точки пересечения клеток- и я так и сделал!

ну
так как ответ уже давно дан итак все понятно я напишу ток об одном! те кто может с дуру моментально видеть стерео картинки без подготовки тот увидит что гипотенузы не прямы линии! у верхнего она выпирает наружу! у второго вогнута во внутрь

А не проще выполнить инструкции задачи?
Я так и сделал, сравнил и никакого "лишнего" квадратика не оказалось.

:)
Это задачка у племенника в 4 классе, только фигуры цветные. Если вырезать из бумаги, то все сходиться. Нет тут кривизны и т.п. Большой и малый треугольники меняються местами и раздвигаем кривые фигурки. Кто не уверен, ножници и бумагу в руки и как детки в 4 классе. А кто проценты выщитывает, жаль вас :)

блин это анекдот

После того, как вырезанный фрагмент перемещается, остается дыра в 6 клеток. Точно столько же клеток образовались с двойным слоем бумаги. Никакого "лишнего" квадратика" и никакой экономии бумаги в помине нет. Люди от большого ума насмотрелись различных популярных примеров иллюзии, и теперь они им мерещатся во всем. Таких легко купить.